Chapter 3 Basic instructions
3.1 Descriptive statistics and summaries
There are a large number of functions in the basic installation of R. It would be practically impossible to see all of them so we will see some of the most used, although we must remember that not only is there the possibility of using predesigned functions, but R also offers the possibility to create your own functions.
Below are some of the basic statistical functions that we can find in R. These functions are generally applied matrix-array or data.frame data objects. Some of them can be applied to the whole table and others to single columns or rows.
sum()Add values.max()Returns the maximum value.min()Returns the minimum value.mean()Calculates the mean.median()Returns the median.sd()Calculates the standard deviation.summary()Returns a statistical summary of the columns.
We are going to applie them using some example data. We will use the data stored in the file fires.csv, inside the Data folder (Table 3.1). This file contains data on the annual number of fires between 1985 and 2009 in several European countries.
Figure 3.1: Structure of the fires.csv file.
The first thing is to import the file into a table.
fires<-read.table('Data/fires.csv', header= TRUE, sep=',')Once data is imported we can take a look at the structure to make sure that everything went well. We should have integer values for each region:
str (fires)## 'data.frame': 25 obs. of 7 variables:
## $ YEAR : int 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 ...
## $ PORTUGAL: int 8441 5036 7705 6131 21896 10745 14327 14954 16101 19983 ...
## $ SPAIN : int 12238 7570 8679 9247 20811 12913 13531 15955 14254 19263 ...
## $ FRANCE : int 6249 4353 3043 2837 6763 5881 3888 4002 4769 4618 ...
## $ ITALY : int 18664 9398 11972 13588 9669 14477 11965 14641 14412 11588 ...
## $ GREECE : int 1442 1082 1266 1898 1284 1322 858 2582 2406 1763 ...
## $ EUMED : int 47034 27439 32665 33701 60423 45338 44569 52134 51942 57215 ...Now we will calculate some descriptive statistics for each column to have a first approximation to the distribution of our data. To do this we will use the function summary() that will return some basic statistical values such as:
- Quantile
- Mean
- Median
- Maximum
- Minimum
summary(fires)## YEAR PORTUGAL SPAIN FRANCE
## Min. :1985 Min. : 5036 Min. : 7570 Min. :2781
## 1st Qu.:1991 1st Qu.:14327 1st Qu.:12913 1st Qu.:4002
## Median :1997 Median :21870 Median :16771 Median :4618
## Mean :1997 Mean :20848 Mean :16937 Mean :4907
## 3rd Qu.:2003 3rd Qu.:26488 3rd Qu.:20811 3rd Qu.:6249
## Max. :2009 Max. :35697 Max. :25827 Max. :8005
## ITALY GREECE EUMED
## Min. : 4601 Min. : 858 Min. :27439
## 1st Qu.: 7134 1st Qu.:1322 1st Qu.:45623
## Median : 9540 Median :1486 Median :55215
## Mean : 9901 Mean :1656 Mean :54249
## 3rd Qu.:11965 3rd Qu.:1898 3rd Qu.:62399
## Max. :18664 Max. :2582 Max. :75382The summary() function is not only used to obtain summaries of data through descriptive statistics, but can also be used in model type objects to obtain a statistical summary of the results, coefficients, significance … Later we will see an example of this applied on a linear regression model.
Let’s now see what happens if we apply some of the functions presented above. Try running the following instructions:
sum(fires)## [1] 2762377max(fires)## [1] 75382min(fires)## [1] 858As can be seen these 3 instructions work with a tablebut mean(), median() and sd() will not. We have to apply them to a single column:
mean(fires$SPAIN)## [1] 16937.24median(fires$SPAIN)## [1] 16771sd(fires$SPAIN)## [1] 5260.5193.2 The apply() function
So far we have seen how to apply some of the basic statistical functions to our data, applying those functions to the data contained in the matrix or some of its columns. In the case of columns we have manually specified which one to apply a function. However, we can apply functions to all elements of an array (columns or rows) using iteration functions.
The apply() function allows you to apply a function to all elements of a table. We can apply some of the functions before the rows or columns of an array. There are different variants of this function. First, as always, invoke the help of the function to make sure what we are doing.
help(apply)According to the specified in the function help we can see that the apply () function works as follows:
apply (X, MARGIN, FUN, …)
Where:
- X: data matrix.
- MARGIN: argument to specify whether the function is applied to rows (1) or columns (2).
- FUN: function to be applied (
mean,sum…)
For example, if we want to sum the values of each country/region we will do as follows:
apply(fires,2,mean)## YEAR PORTUGAL SPAIN FRANCE ITALY GREECE EUMED
## 1997.00 20848.20 16937.24 4907.16 9900.64 1655.80 54249.04Well, almost there. We have included the YEAR column which is the first one:
apply(fires[,-1],2,mean)## PORTUGAL SPAIN FRANCE ITALY GREECE EUMED
## 20848.20 16937.24 4907.16 9900.64 1655.80 54249.04EXERCISE 1: Calculate the total number of fires on a yearly basis.
Deliverables:
- Write a text file (.txt) with the result.
EXERCISE 2: - Open the file “barea.csv” and save it in an object named “barea” - Select and store in a new matrix the data from the year 2000 to 2009. - Calculate descriptive statistics 2000-2009. - Calculate the mean, standard deviation, minimum and maximum of all columns and save it to a new object.
Hint: use the apply function to calculate each statistic, separately.
Deliverables:
- Write a text file (.txt) with the result.
3.3 Installing packages
We have already seen how some of the basic functions of R. work. However, we have the possibility of extending the functionalities of R by importing new packages into our environment. These packages are developed by different research groups and/or individuals.
There are currently over 4600 packages available in the R project repository (CRAN). Obviously we do not need to know how each one of them works, but only focus on those that fit our needs.
The import and installation of new packages is carried out in 2 stages:
- obtaining and installing and internal call to the package.
- Loading the package into our session.
3.3.1 Installing an external package
We will install the “foreign” package. This package provides functions for reading and writing data stored in different statistical software formats such as Minitab, S, SAS, SPSS, Stata, Systat … and to read and write dBase files such as attribute tables of vector layers in format shapefile. The first thing we will do is get the package via download. This can be done from the menu of R:
- Packages / Install packages …
- Select download directory (mirror)
- Search for “foreing”
If you are using RStudio simply go to the Packages tab in the lower right box and select the Install option. In the popup window select the Repository (CRAN, CRANextra) option in the drop-down menu and type the name of the package.
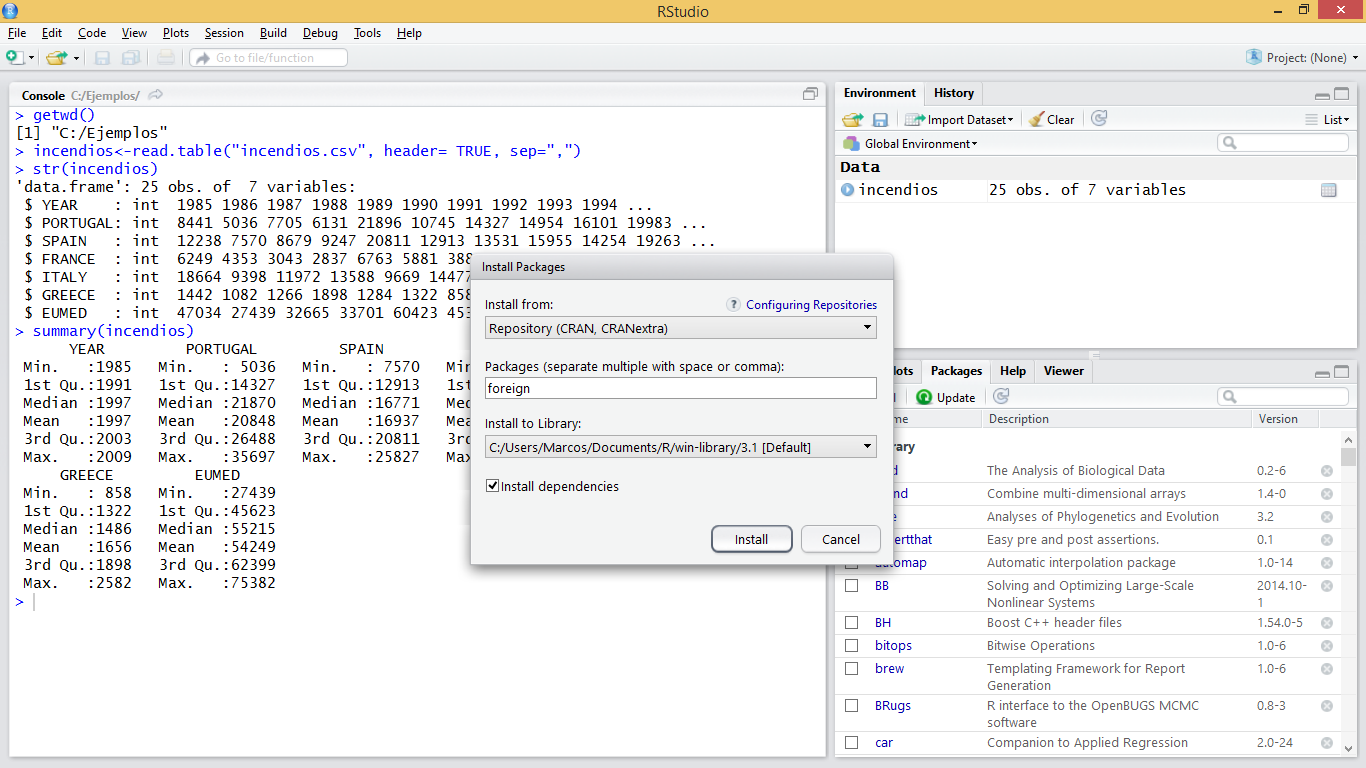
Figure 3.2: Installing a package using RStudio
Another option is to obtain the package in .zip format directly from the webpage of project R and use the function Install package (s) from local zip files … (or Package archives in RStudio).
It is also possible to install packages through instructions in the R window, which is the most recommended method7:
#install.packages('foreign')At this point we would have installed the package in our personal library of R. However, in order to use the functions of the new package in our R environment it is necessary to make an internal call to the package. This is generally done using the library() function8:
library(foreign)Once this is done we have all the functions of the package ready to be used. All that is left is to learn how to use the functions of the package… which is easy to say but maybe not to do.
3.4 Create a function
So far we have mainly seen how to use pre-designed functions either in the default installation or from other packages. However, there is the possibility of creating our own functions.
A function is a group of instructions that takes an input or input data, and uses them to calculate other values, returning a result or product. For example, the mean() function takes as input a vector and returns as a result a numeric value that corresponds to the arithmetic mean.
To create our own functions we will use the object called function that constitute new functions. The usual syntax is:
FunctionName <- function (arguments){commands}
Where:
argumentsare the arguments we want to pass to our function.commandsare the instructions needed to do whatever the function does.
Let’s look at a simple example. We will create a function to calculate the standard deviation of a vector with numerical data. The standard deviation formula looks like this:
Which is essentally the square root (sqrt()) of the variance (var()):
desv <- function(x){sqrt(var(x))}The function name is desv(). This function requires a single argument (x) to be executed. Once the function is defined, it can be called and used as any other predefined function in the system.
data <- 1:10
desv(data)## [1] 3.02765Let’s see an example with 2 arguments. We will create a function to calculate the NDVI. The function will take as arguments two objects of vector type corresponding to the sensor Landsat TM channels 3 and 4:
The normalized difference vegetation index (NDVI) is a simple graphical indicator that can be used to analyze remote sensing measurements, typically but not necessarily from a space platform, and assess whether the target being observed contains live green vegetation or not wikipedia.org.
Where (y) is the near-infrarred band and (x) is the red band.
ndvi <- function(x,y){(y-x)/(y+x)}As we have said, once created we can use our functions in the same way as the rest of functions. This includes using the apply() function and its derived versions to iterate over rows and columns of an array or dataframe.
Let’s see an example with the function desv(), previously created applied to the data of number of fires:
apply(fires,2,desv)## YEAR PORTUGAL SPAIN FRANCE ITALY
## 7.359801 9187.114305 5260.519400 1393.670265 3467.510729
## GREECE EUMED
## 496.662025 13547.393887